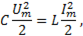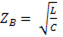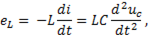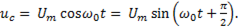К вопросу о индуктивной фазе разряда конденсатора на индуктивность.
Разрядка конденсатора на индуктивность
Рассмотрим явления в
– цепи, представленной рис. , когда конденсатор, заряженный до напряжения
замыкается на идеальную катушку .
В начальный момент времени напряжение на конденсаторе имеет наибольшее значение, и в электрическом поле конденсатора запасена энергия
(11-21)
При замыкании рубильника конденсатор начнет разряжаться, и в цепи возникает электрический ток. Вместе с током создается магнитное поле, а следовательно, и эдс самоиндукции, которая в каждый момент равна и противоположна напряжению на конденсаторе, так как для этой цепи по второму закону Кирхгофа справедливо соотношение
(11-22)
Так как
то
и следовательно, ток в цепи нарастает со скоростью
По мере того как конденсатор разряжается и напряжение падает, уменьшается и скорость нарастания тока пока, наконец, она не упадет до нуля.
Но, с другой стороны, при
равна нулю и энергия электрического поля конденсатора. Так как в рассматриваемой цепи энергия не превращается в тепло, то первоначальный запас энергии переходит в энергию магнитного поля катушки. Отсюда следует. Что при
ток в цепи имеет наибольшее значение; его можно найти, приравняв первоначальный запас энергии тому значению магнитной энергии, которое имеет место при наибольшем токе:
откуда
(11-23)
Величина
имеет размерность сопротивления и называется
волновым сопротивлением.
Рис.139
Разрядный ток (рис.139)
Следовательно эдс самоиндукции
подставив это выражение в ( ), получаем дифференциальное уравнение LC- цепи
(11-24)
Решением этого уравнения является выражение следующего вида:
(11-15)
Ток в цепи
(11-26)
Таким образом, в цепи протекает синусоидальный ток, и напряжение на конденсаторе изменяется периодически, хотя источник переменного тока в цепи отсутствует.
Процесс уменьшения напряжения конденсатора от первоначального значения до нуля соответствует переносу электронов с отрицательной обкладки на положительную. Разрядкой конденсатора этот процесс не заканчивается, так как ток в катушке не может меняться скачком. В цепи продолжает протекать ток прежнего направления, но уменьшающийся по величине. Наличие этого тока означает перенос электронов с электрода, бывшего ранее отрицательным, на электрод, бывший ранее положительным, благодаря чему первый начнет заряжаться положительно, а второй – отрицательно.
При отсутствии в цепи сопротивления R этот процесс будет продолжаться до тех пор, пока конденсатор не зарядится до напряжения, по величине равного начальному, но обратного по знаку. Далее конденсатор начнет разряжаться в обратном направлении, а затем снова заряжаться, и этот процесс будет продолжаться до тех пор, пока цепь не будет разомкнута.
Таким образом, в рассматриваемой цепи энергия электрического поля переходит в энергию магнитного поля, и наоборот, т.е. в цепи происходят незатухающие периодические колебания энергии.
Угловая частота этих свободных гармонических колебаний определяется индуктивностью и емкостью рассматриваемой LC – цепи.
 Жесть..............
Жесть..............